"dontbethatguy" (dontbethatguy2)
01/13/2015 at 22:23 • Filed to: None
0
7|
"dontbethatguy" (dontbethatguy2)
01/13/2015 at 22:23 • Filed to: None | 0
| 7 |
Good evening Opponauts!! Welcome to this week's edition of the Oppo Ebay Challenge. This week: find the combination of sportscar, hot-hatch, and sedan for $136,000 or less that cost the highest amount of money/second which would mean you want to find the fastest cars that cost the least amount of money. Hopefully this can be a weekly thing and if there is enough interest I will compile a follow-up post with the top 10 suggestions.
Rules:
1. Must be stock and street legal. If the car is modified it should be treated as unmodified for the sake of comparison.
2. All laptimes must come from reputable sources.
3. Listings must have a reasonable chance of selling for the price given.
My 3:
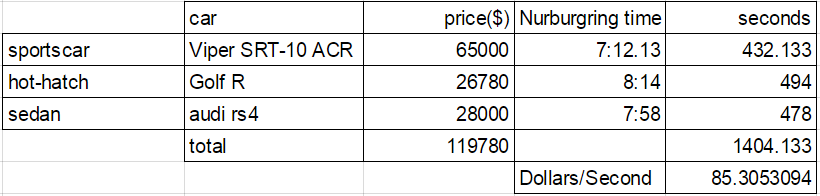
Now lets see how well you guys can do! Happy Hunting!
Rainbow
> dontbethatguy
01/13/2015 at 22:34 |
|
But this means that the slower it is, the lower the money-per-second is.
Trunk Impaired 318
> dontbethatguy
01/13/2015 at 22:48 |
|
Sports car- E46 M3 $9500 8:22
Hot Hatch- VW R32 $10000 8:36
Sedan- Cadillac CTS-V $26000 7:59
$45500/1497 seconds = $30.4/s
|
dontbethatguy
> Rainbow
01/13/2015 at 22:50 |
|
Edited. It should be most not least. Thanks.
Local Miata Bro
> dontbethatguy
01/14/2015 at 01:25 |
|
Fuck your rules I want this. I've seen it run laps around gt3s and z06s
https://stlouis.craigslist.org/cto/4827429859…
briannutter1
> dontbethatguy
01/14/2015 at 10:32 |
|
All pricing from autotrader (usually 2nd or 3rd from cheapest example) and all cars available in the USA. 2006+ C6z 7.22.68 (cup tires off the later cars) $31,950. 2010+ STI..(very hard to find old used examples so going with $35k) lapped the ring in 2010 at 7:55:00. 2009+ Caddy CTS-V laptime 7.59.32 at $28,300. Total Dollars $95,250. Total laptime seconds 1397. $68.18/second.
|
dontbethatguy
> Local Miata Bro
01/14/2015 at 12:20 |
|
That... is perfectly acceptable. That is one sweet car.
Eazy-O
> dontbethatguy
01/14/2015 at 12:55 |
|
I don't think your comparison makes sense.
Basically you're asking what's the most expensive way to go... fastest.
The car with the least seconds and highest price will get the highest amount of dollars per second . So if we have two cars that are equally fast, while one is twice the price, the doubly expensive one will have the highest ratio.
Your equation would sorta work in a different manner, though:
[PRICE] × [TIME] =[RATIO]
The lower this ratio, the lower the time and price, which you want. :) There are better ways of going about this, but, eh.